Bind Mesh Reconstruction for Correctives

Standard Skinning Deformation

Most of the time in games, we are looking to deform a mesh driven by a particular skeletal pose which has been changed from the bind pose. We have a bind mesh which lines up to this bind pose of the skeleton, and we can use the skinning equation to solve for the deformed mesh – pretty straight-forward:

\[\begin{equation} \mathbf{v'}=\sum_{j=1}^{N}w_{j}\mathbf{v}_{b}\mathbf{K}_{j} \end{equation}\]

Where:

• \(\mathbf{v'}\) is the deformed vertex position
• \(N\) is the number of influences that we are skinning each vert to
• \(w_{j}\) is the skin weight between this vertex and joint \(j\)
• \(\mathbf{v}_{b}\) is the bind-pose vertex position

• \(\mathbf{K}_{j}\) is the skinning matrix for the joint j, which is the inverse bind pose matrix * the current/deformed pose matrix for the joint:

  \[\mathbf{K}_{j}=\mathbf{B}_{j}^{-1}\mathbf{D}_{j}\]

  where \(\mathbf{B}_{j}^{-1}\) is the inverse bind pose matrix for the joint j, and \(\mathbf{D}_{j}\) is the deformed transform matrix for joint j.

We can easily demonstrate this process in Maya anytime we skin a mesh to skeleton, and then start moving the skeleton around. Maya conveniently lets us revert back to the undeformed mesh via the “Go to Bind Pose” command.

Inverse deformation

However, there are times where we need to model a mesh after it’s been deformed. For example, when using blendshapes in games, we often need to create corrective blendshapes that fix problems when two or more shapes combine poorly. Or perhaps you are building body customization that pushes the limits of the skinned geometry, and you need to smoothly blend in alternate geometry past a certain point. In both of these cases, we’ll need to make the changes in the deformed pose, but export back to engine in the original bind pose.

You might think that you can simple bind the new mesh to the deformed pose, and then deform “back” to the original bind pose, but the math doesn’t work because skinning is not bi-directional.

In this case, we need to remodel the mesh without skin weights in Maya, copy the weights back onto it, reconstruct the equivalent bind mesh, and then re-export the new bind mesh to engine to be used as a corrective shape. However, we have no good way in Maya to reconstruct this bind mesh out of the box in Maya*, but with a bit of simple math and Maya API code, we can do this pretty easily.

*3dsmax allows you to make model edits on a skinned model and will affect the original bind mesh simultaneously, making this much easier.

Solving for Bind Vertices

In order to do this, we just need to solve for \(\mathbf{v}_{b}\).

Since we know that:

\[\begin{equation} \mathbf{v'}=\sum_{i=1}^{N}w_{i}\mathbf{v}_{b}\mathbf{K}_{i} \end{equation}\]

We can also rearrange this to:

\[\begin{equation} \mathbf{v'}=\mathbf{v}_{b}\sum_{i=1}^{N}w_{i}\mathbf{K}_{i} \end{equation}\]

and then multiply by the inverse:

\[\begin{equation} \mathbf{v}_{b}=\mathbf{v'}\left(\sum_{i=1}^{N}w_{i}\mathbf{K}_{i}\right)^{-1} \end{equation}\]

Now that we have the simple math, we just need to write something up using Maya API.

Code Sample

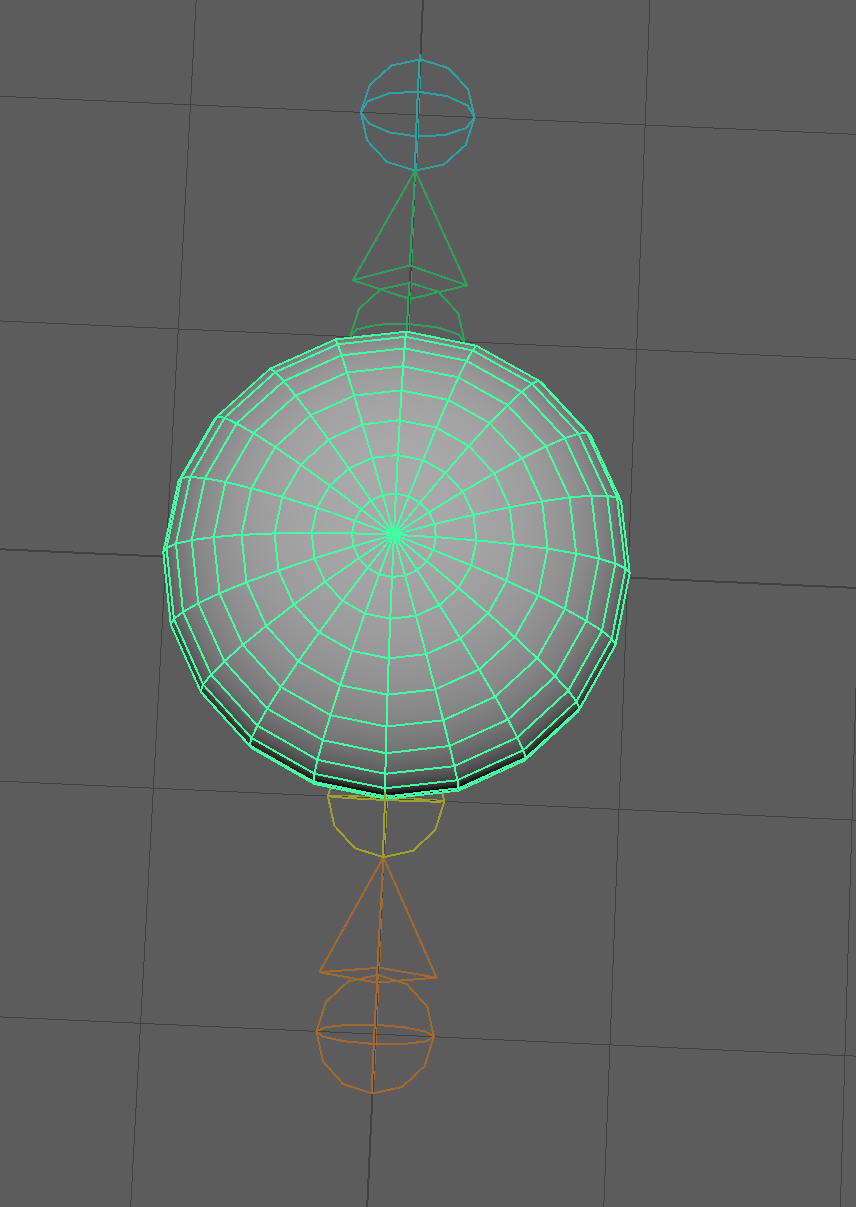
Let’s suppose we have a sphere that’s been skinned to a simple joint chain.

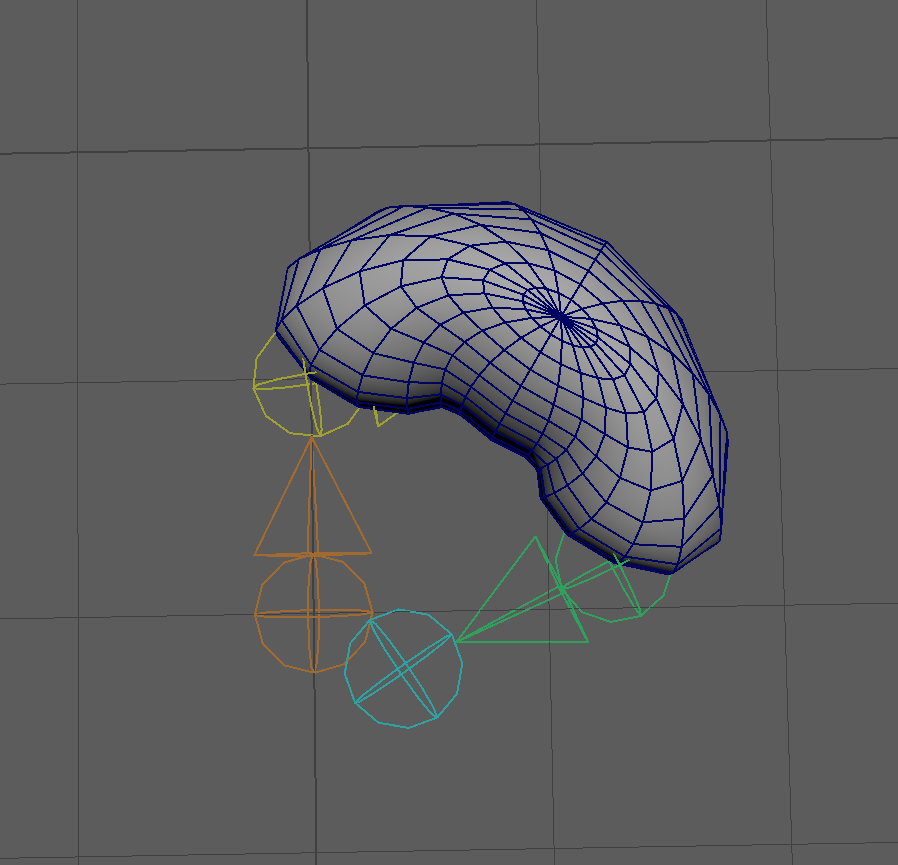
The joint chain has been posed, which has deformed the sphere, but if we’ve modified the sphere geometry and lost the history, we don’t have any updated bind mesh.

You might think that you can simply rebind the mesh to the deformed pose, and see what happens when you move the joints back to the bind pose, but you can see quite clearly that won’t get you what you’re looking for:

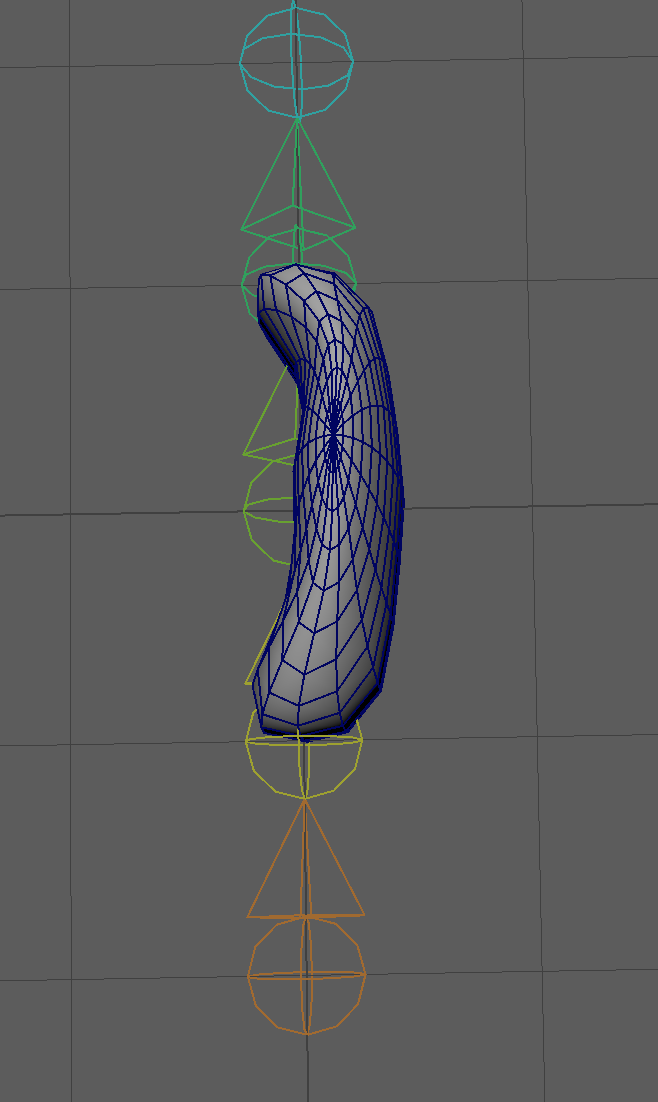
However, with the method we talked about, we can reconstruct the bind mesh given the following information:

• The deformed mesh
• The skin weights
• The bind pose of the skeleton
• The new pose of the skeleton

Here is the main part of the code, which does the actual reconstruction of the mesh, given a deformed mesh (with skin, but improper bind pose), and two skeleton poses (one is the bind pose, one is the current pose).

Overall, you can see this is a pretty simple operation.

bind_verts = []
vertex_index = 0
print("Reconstructing {} vertices".format(num_vertices))
for i in range(0, len(weights), num_influences):
    cur_vertex = source_points[vertex_index]
    vertex_weights = weights[i:i + num_influences]
    weighted_skin_matrix = om.MMatrix([0.0] * 16)
    for j, weight in enumerate(vertex_weights):
        if weight > 0.0:
            joint_name = joints[j]
            current_joint_matrix = cached_deformed_pose[joint_name]                   
            bind_joint_matrix = cached_bind_pose[joint_name]
            skin_matrix = bind_joint_matrix.inverse() * current_joint_matrix
            weighted_skin_matrix += weight * skin_matrix
    bind_vertex = cur_vertex * weighted_skin_matrix.inverse()
    bind_verts.append(bind_vertex)
    vertex_index += 1
    
duplicate_mesh_fn.setPoints(bind_verts, space=om.MSpace.kWorld)

# Now, we want to bind the new mesh to the original bind pose, and copy weights by index
cmds.currentTime(bind_pose_time)
cmds.select(clear=True)
weights, influence_indices = get_skin_weights(skin_cluster_name)
target_skin_cluster_name = cmds.skinCluster(joints, duplicate_mesh, toSelectedBones=True, bindMethod=0, skinMethod=0)[0]
set_skin_weights(target_skin_cluster_name, weights, influence_indices)

For the full code and example scene, see Bind Mesh Reconstruction